La gamme de Pythagore (musique)
Qu’est-ce que la gamme de Pythagore?
Pythagore, mathématicien grec de l’Antiquité, était convaincu que tout phénomène pouvait être expliqué uniquement par les nombres naturels. Il a donc entrepris l’étude mathématique de la gamme musicale grecque sur le monocorde. À cette époque, la monodie (émission d’un son unique) était pratiquée. Mais les connaissances mathématiques de l’époque et leur rapport aux notes lui permirent de diviser une octave en sept notes, qui n’étaient pas régulièrement espacées en fréquence. Pourtant, cette gamme fut utilisée jusqu’au 17e siècle.
On appelle intervalle entre deux notes le rapport (et non la différence) de la fréquence fondamentale de chacune. Les rapports 3/2, 2/1, 4/3 sont jugés consonants, alors que le rapport 7 est considéré comme dissonant.
On appelle octave un intervalle de valeur égal à 2. Par exemple, la note La4 qui a pour fréquence 880 Hz est à l’octave de la note La3 qui a pour fréquence 440 Hz : la fréquence du La4 est deux fois plus grande que celle du La3.
On appelle gamme l’ensemble des notes comprises dans une octave. Construire une gamme consiste à choisir une série de notes à l’intérieur d’une octave, ayant entre elles des propriétés de consonance.
À partir de son monocorde, Pythagore aurait choisi de prendre :
- La moitié de la corde qui correspond à une octave
- Les 2/3 de la corde (car 1/3 n’est pas compris entre 1/2 et 1, et impose de prendre la note à l’octave inférieure)
Les fractions 1/2 et 2/3 donnent des sons consonants. Puisque la corde de longueur 2/3 donne des sons consonants, il choisit les « 2/3 des 2/3 » pour avoir la même impression avec la corde de 2/3. On obtient ainsi une corde de longueur 4/9. Mais ce nombre n’est pas compris dans l’octave choisie (1/2 et 1). Il prend donc le même son, mais à l’octave supérieure, c’est-à-dire en multipliant par 2 : soit 89.
Prenons, à présent, les « 2/3 des 8/9 », soit 23×89=1627.
Et ainsi de suite, on obtient les 7 premières fractions : 1→2/3→8/9→16/27→64/81→128/243→512/729→2048/2187.
La 5e fraction 128/243 est proche de 1/2. La 7e fraction 2048/2187 est plus proche de 1 que toutes les précédentes : on peut considérer qu’on a quasiment bouclé la boucle. La 4e fraction 64/81 est proche de ¾. D’où les rapports de la gamme de Pythagore qui s’est arrêté à la 7e fraction.
En pinçant une corde au tiers (donc en la divisant par 3), il reconnaît le rapport de quinte. Si l’intervalle entre deux notes vaut 3/2, alors elles sont en rapport de quinte. De même diviser la corde par 4 et faire vibrer les ¾ revient à parler de rapport de quarte. Si l’intervalle entre deux notes vaut 4/3, alors elles sont en rapport de quarte. Par conséquent, Pythagore part du principe que la quinte de la quinte forme un intervalle consonant avec la note de départ, il crée ainsi un accord fait par l’enchaînement de quintes justes : d’où le nom de « cycle des quintes ».
Prenons la note Do comme note de départ et calculons un cycle de sept quintes :
| Note | Do | Sol | Ré | La | Mi | Si | Fa | Do |
| Intervalle par rapport au Do | 1 | 3/2 | (3/2)^2 | (32)^3 | (32)^4 | (32)^5 | (32)^6 | (32)^7 |
| Fraction | 1 | 3/2 | 9/4 | 27/8 | 81/16 | 243/32 | 729/64 | 218/7128 |
| Valeur approchée | 1 | 1,5 | 2,25 > 2 | 3,37 > 2 | 5,06 > 2 | 7,59 > 2 | 11,4 > 2 | 17,09 > 2 |
| Fraction ramenée à l’octave étudiée | 1 | 3/2 | 9/8 | 27/16 | 81/64 | 243/128 | 729/512≈4/3 | 2187/1024≈2,14≈2 |
Pythagore mit en place les intervalles consonants de base : l’octave correspond au rapport 2/1 et la quinte au rapport 3/2. La quarte étant une quinte descendante suivie d’une octave correspond à l’intervalle 2/3 × 2 = 4/3.
La gamme de Pythagore est donc la suivante :
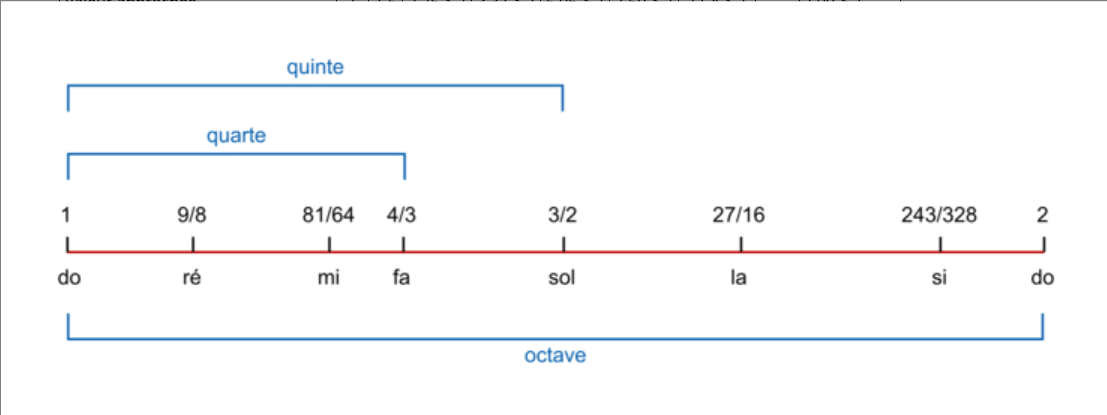
L’inconvénient de la gamme de Pythagore est que les notes n’ont pas des intervalles constants et de ce fait, un morceau de musique qui commencerait par un « La » ne serait pas transposable à un « Fa » : il sonnerait faux. On ne peut donc pas modifier d’un même intervalle la fréquence de toutes les notes d’un morceau pour le transposer dans une tonalité différente.
Les deux Do devraient être situés à 4 octaves l’un de l’autre, mais (32)^7=2187/128≈17≠24. Le Do créé en prenant sept quintes successives n’est pas vraiment un Do, mais s’en rapproche. On a presque un cycle de sept notes. L’intervalle entre le Do obtenu et le Do théorique est appelé un « comma ». On dit que le cycle des quintes formées par sept notes boucle presque sur la note de départ.
Le cycle des quintes comportant sept notes comporte six quintes justes et une quinte fausse.






